Différence entre différentiel et dérivé

Pour mieux comprendre la différence entre le différentiel et la dérivée d'une fonction, vous devez d'abord comprendre le concept d'une fonction.

Une fonction est l'un des concepts de base en mathématiques qui définissent une relation entre un ensemble d'entrées et un ensemble de sorties possibles où chaque entrée est liée à une sortie. Une variable est la variable indépendante et l'autre variable est la variable dépendante.

Le concept de fonction est l'un des sujets les plus sous-estimés en mathématiques mais est essentiel pour définir des relations physiques. Prenons par exemple: l'énoncé «y est une fonction de x» signifie que quelque chose lié à y est directement lié à x par certaines formules. Disons si l'entrée est 6 et que la fonction est d'ajouter 5 à l'entrée 6. Le résultat sera 6 + 5 = 11, qui est votre sortie.

Il y a quelques exceptions en mathématiques ou vous pouvez dire des problèmes, qui ne peuvent pas être résolus par des méthodes ordinaires de géométrie et d'algèbre seule. Une nouvelle branche des mathématiques connue sous le nom de calcul est utilisée pour résoudre ces problèmes.

Le calcul est fondamentalement différent des mathématiques qui non seulement utilisent les idées de la géométrie, de l'arithmétique et de l'algèbre, mais traite également du changement et du mouvement.

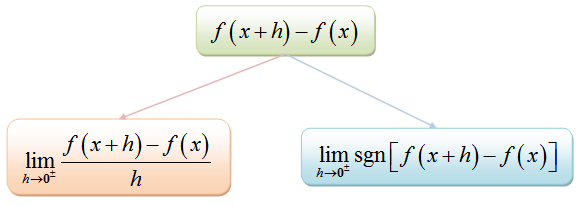
Le calcul en tant qu'outil définit la dérivée d'une fonction comme limite d'un type particulier. Le concept de dérivé d'une fonction distingue le calcul des autres branches des mathématiques. Le différentiel est un sous-champ de calcul qui fait référence à la différence infinitésimale dans une quantité variable et est l'une des deux divisions fondamentales du calcul. L'autre branche est appelée calcul intégral.

Qu'est-ce que le différentiel?

Le différentiel est l'une des divisions fondamentales du calcul, ainsi que le calcul intégral. C'est un sous-champ de calcul qui traite du changement infinitésimal dans une quantité variable. Le monde dans lequel nous vivons est plein de quantités interdépendantes qui changent périodiquement.

Par exemple, la zone d'un corps circulaire qui change à mesure que le rayon change ou un projectile qui change avec la vitesse. Ces entités changeantes, en termes mathématiques, sont appelées variables et le taux de changement d'une variable par rapport à un autre est un dérivé. Et l'équation qui représente la relation entre ces variables est appelée une équation différentielle.

Les équations différentielles sont des équations qui contiennent des fonctions inconnues et certaines de leurs dérivés.

Qu'est-ce que le dérivé?

Le concept de dérivé d'une fonction est l'un des concepts les plus puissants en mathématiques. La dérivée d'une fonction est généralement une nouvelle fonction qui est appelée fonction dérivée ou la fonction de vitesse.

La dérivée d'une fonction représente un taux de variation instantané de la valeur d'une variable dépendante par rapport à la variation de la valeur de la variable indépendante. C'est un outil fondamental du calcul qui peut également être interprété comme la pente de la ligne tangente. Il mesure à quel point le graphique d'une fonction est raide à un moment donné sur le graphique.

En termes simples, le dérivé est la vitesse à laquelle la fonction change à un moment donné.

Différence entre différentiel et dérivé

Définition du différentiel vs. Dérivé

Les termes différentiels et dérivés sont intimement liés les uns aux autres en termes d'interrelation. En mathématiques, l'évolution des entités est appelée variables et le taux de changement d'une variable par rapport à un autre est appelé dérivé.

Les équations qui définissent la relation entre ces variables et leurs dérivés sont appelées équations différentielles. La différenciation est le processus de recherche d'un dérivé. La dérivée d'une fonction est le taux de variation de la valeur de sortie par rapport à sa valeur d'entrée, tandis que le différentiel est le changement réel de fonction.

Relation de différentiel vs. Dérivé

La différenciation est une méthode de calcul d'une dérivée qui est le taux de changement de la sortie y de la fonction par rapport au changement de la variable x.

En termes simples, la dérivée se réfère au taux de changement de y par rapport à x, et cette relation est exprimée en y = f (x), ce qui signifie que y est fonction de x. La dérivée de la fonction f (x) est définie comme la fonction dont la valeur génère la pente de f (x) où elle est définie et f (x) est différenciable. Il fait référence à la pente du graphique à un moment donné.

Représentation de différentiel vs. Dérivé

Les différences sont représentées comme dX, dy, dt, et ainsi de suite, où dx représente un petit changement de x, dy représente un petit changement en y, et dt est un petit changement de t. Lors de la comparaison des changements dans les quantités connexes où y est la fonction de x, le différentiel dy peut être écrit comme:

dy = f^'(X) dX

La dérivée d'une fonction est la pente de la fonction à tout moment et est écrite comme d/ /dX. Par exemple, le dérivé du péché (x) peut être écrit comme:

d/ /dx sin (x) = sin (x)^' = cos (x)

Différentiel vs. Dérivé: tableau de comparaison

Résumé du différentiel vs. Dérivé

En mathématiques, le taux de changement d'une variable par rapport à une autre variable est appelé dérivé et les équations qui expriment la relation entre ces variables et leurs dérivés sont appelées équations différentielles. En un mot, les équations de différencia impliquent des dérivés qui spécifient en fait comment une quantité change par rapport à un autre. En résolvant une équation différentielle, vous obtenez une formule pour la quantité qui ne contient pas de dérivés. La méthode de calcul d'une dérivée est appelée différenciation. En termes simples, la dérivée d'une fonction est le taux de variation de la valeur de sortie par rapport à sa valeur d'entrée, tandis que le différentiel est le changement réel de fonction.