Différence entre les intégrales définies et indéfinies
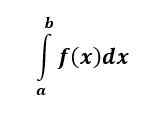
- 1786
- 438
- Juliette Paul
Le calcul est une branche importante des mathématiques et la différenciation joue un rôle essentiel dans le calcul. Le processus inverse de la différenciation est connu sous le nom d'intégration, et l'inverse est connu comme l'intégrale, ou tout simplement, l'inverse de la différenciation donne une intégrale. Sur la base des résultats, ils produisent les intégrales sont divisées en deux classes à savoir., intégrales définies et indéfinies.
Intégrale définie
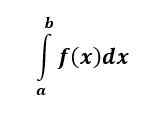
L'intégrale définie de f (x) est un nombre et représente la zone sous la courbe f (x) depuis x = a pour x = b.
Une intégrale définie a des limites supérieures et inférieures sur les intégrales, et elle est appelée définie parce que, à la fin du problème, nous avons un nombre - c'est une réponse définitive.
Intégral indéfini
L'intégrale indéfinie de f (x) est une fonction et répond à la question: «Quelle fonction lors de la différenciation donne f (x)?"
Avec une intégrale indéfinie, il n'y a pas de limites supérieures et inférieures à l'intégrale ici, et ce que nous obtiendrons est une réponse qui a encore Xest dedans et aura également une constante (généralement indiquée par C) dans elle.
Une intégrale indéfinie donne généralement une solution générale à l'équation différentielle.
L'intégrale indéfinie est davantage une forme générale d'intégration, et elle peut être interprétée comme l'anti-dérivé de la fonction considérée.
Supposons la différenciation de la fonction F conduit à une autre fonction F, Et l'intégration de F donne l'intégrale. Symboliquement, ceci est écrit comme
F (x) = ∫ƒ (x) dx
ou
F = ∫ƒ dx
où les deux F et ƒ sont des fonctions de X, et F est différenciable. Dans la forme ci-dessus, il est appelé Reimann intégral et la fonction résultante accompagne une constante arbitraire.
Une intégrale indéfinie produit souvent une famille de fonctions; Par conséquent, l'intégrale est indéfini.
Les intégrales et le processus d'intégration sont au cœur de la résolution d'équations différentielles. Cependant, contrairement aux étapes de la différenciation, les étapes d'intégration ne suivent pas toujours une routine claire et standard. Parfois, nous voyons que la solution ne peut pas être exprimée explicitement en termes de fonction élémentaire. Dans ce cas, la solution analytique est souvent donnée sous la forme d'une intégrale indéfinie.
Théorème fondamental du calcul
L'intégrale définie et indéfinie sont liées par le théorème fondamental du calcul comme suit: afin de calculer un Intégrale définie, trouvez le intégral indéfini (également connu sous le nom d'anti-dérivé) de la fonction et évaluer aux points de terminaison x = a et x = b.
La différence entre les intégrales définies et indéfinies sera évidente une fois que nous aurons évalué les intégrales pour la même fonction.
Considérez l'intégrale suivante:
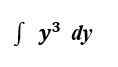
D'ACCORD. Faisons-les deux et voyons la différence.
Pour l'intégration, nous devons en ajouter un à l'indice qui nous conduit à l'expression suivante:
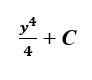
À ce moment C est simplement une constante pour nous. Des informations supplémentaires sont nécessaires dans le problème pour déterminer la valeur précise de C.
Évaluons la même intégrale dans sa forme définie I.e., avec les limites supérieures et inférieures incluses.
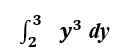
Graphiquement parlant, nous informons maintenant la zone sous la courbe f (x) = y3 entre y = 2 et y = 3.
La première étape de cette évaluation est la même que l'évaluation intégrale indéfinie. La seule différence est que cette fois-ci, nous n'ajoutons pas la constante C.
L'expression dans ce cas ressemble à ce qui suit:
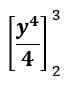
Ce tour mène:
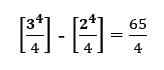
Essentiellement, nous avons substitué 3 puis 2 dans l'expression et obtenu la différence entre eux.
C'est la valeur définie par opposition à l'utilisation de constante C plus tôt.
Explorons le facteur constant (en ce qui concerne l'intégrale indéfinie) plus en détail).
Si le différentiel de y3 est 3Y2, alors
∫3Y2dy = y3
Cependant, 3Y2 pourrait être le différentiel de nombreuses expressions dont certaines comprennent y3-5, y3+7, etc… cela implique que le renversement n'est pas unique car la constante n'est pas comptabilisée pendant l'opération.
Donc en général, 3Y2 est le différentiel de y3+C où C est toute constante. Soit dit en passant, C est connu comme le 'constante d'intégration'.
Nous écrivons ceci comme:
∫ 3Y2.dx = y3 + C
Les techniques d'intégration pour une intégrale indéfinie, telle que la recherche de table ou l'intégration de risque, peuvent ajouter de nouvelles discontinuités pendant le processus d'intégration. Ces nouvelles discontinuités apparaissent parce que les anti-dérivés peuvent nécessiter l'introduction de logarithmes complexes.
Les logarithmes complexes ont une discontinuité de saut lorsque l'argument traverse l'axe réel négatif, et les algorithmes d'intégration ne peuvent parfois pas trouver de représentation où ces sauts annulent.
Si l'intégrale définie est évaluée en calculant d'abord une intégrale indéfinie, puis en substituant les limites d'intégration dans le résultat, nous devons être conscients que l'intégration indéfinie pourrait produire des discontinuités. Si c'est le cas, en outre, nous devons étudier les discontinuités dans l'intervalle d'intégration.

